Grenshoek

Wanneer een lichtbundel vanuit een optisch dichter medium op een grensvlak met een optisch minder dicht medium valt, ontstaat breking van de normaal af. (Bijvoorbeeld wanneer een lichtstraal vanuit diamant naar lucht gaat.) Als de invalshoek van de lichtbundel groter wordt, wordt ook de brekingshoek in sterkere mate groter. Er zal, naarmate de invalshoek groter wordt, een steeds groter deel van de lichtbundel terugkaatsen op het grensvlak, totdat de invalshoek dusdanig is dat de gebroken lichtbundel samenvalt met het grensvlak (dus er precies langs loopt). De invalshoek waarbij de brekingshoek 90º is heet grenshoek g. Is de invalshoek groter dan de grenshoek, dan wordt de bundel volledig teruggekaatst.

Nogmaals, volledige terugkaatsing ontstaat alleen bij breking van de normaal af, dus in het algemeen van vast naar gas, vast naar vloeibaar of van vloeibaar naar gas. Bij de grenshoek g geldt dus dat sin r = sin 90^o = 1

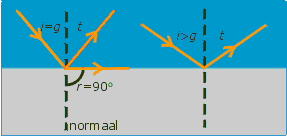
Een paar voorbeelden

Voorbeeld 6

De brekingsindex diamant is 2,42.
- Bereken de grenshoek g voor een lichtbundel die vanuit diamant naar lucht gaat.

Uitwerking:

`n_{"lucht"\rightarrow "diamant"}=2,42 \quad\Rightarrow\quad n_{"diamant" \rightarrow "lucht} = \frac{1}{2,42}=0,413`

Bij de grenshoek g geldt dat i = g en sin r = sin 90º = 1

`n = \frac{\sin i}{\sin r} \quad\Rightarrow\quad 0,413 = \frac {\sin g}{1} \quad\Rightarrow\quad \sin g = 0,413`

`g=\sin^{-1} 0,413 = 24,4^\circ`

Voorbeeld 7

Een lichtstraal valt vanuit water op het grensvlak met lucht.
n_{lucht→water} = 1,33. De invalshoek is 60º.
- Treedt er totale terugkaatsing op?

Uitwerking:
Als de invalshoek groter is dan de grenshoek, dan treedt volledige terugkaatsing op. Wat je dus bij deze opgave moet berekenen is of de invalshoek van 60º groter is dan de grenshoek. De grenshoek bereken je als volgt:

`n_{"lucht" \rightarrow "water"}=1,33 \quad\Rightarrow\quad n_{"water" \rightarrow "lucht"}=\frac {1}{1,33}=0,752`

`0,752 = \frac{\sin g }{ 1} \quad\Rightarrow\quad \sin g=0,752`

`g = \sin^{-1} 0,752 = 48,8^\circ`

Conclusie:
de invalshoek (60º) is groter dan de grenshoek (48,8º), dus er vindt volledige terugkaatsing plaats.

Hierna een paar opgaven om het zelf te proberen. Gebruik eventueel de applet om je antwoorden te controleren.
Opgave 9

De brekingsindex van een bepaald soort glas is 1,50.
- Bereken de grenshoek voor de overgang van dit glas naar lucht.

De brekingsindex voor de overgang van dit soort glas naar lucht is:

`n_{"glas" \rightarrow "lucht"} = \frac{1}{n_{"lucht" \rightarrow "glas"}} = \frac {1}{1,50}=0,667`

Voor de grenshoek geldt dan:

`n=\frac {\sin i}{\sin r} \quad\Rightarrow\quad 0,667=\frac {\sin g}{1} \quad\Rightarrow\quad \sin g=0,667`

`g = \sin^{-1} 0,667 =41,8^\circ`

Opgave 10

De grenshoek voor de overgang van perspex naar water is 63,3º.
- Bereken de brekingsindex voor deze overgang.

Er geldt:

`n = \frac {\sin i}{\sin r} \quad\Rightarrow\quad n=\frac {\sin g}{1} \quad\Rightarrow\quad n = \sin 63,3^\circ = 0,893`